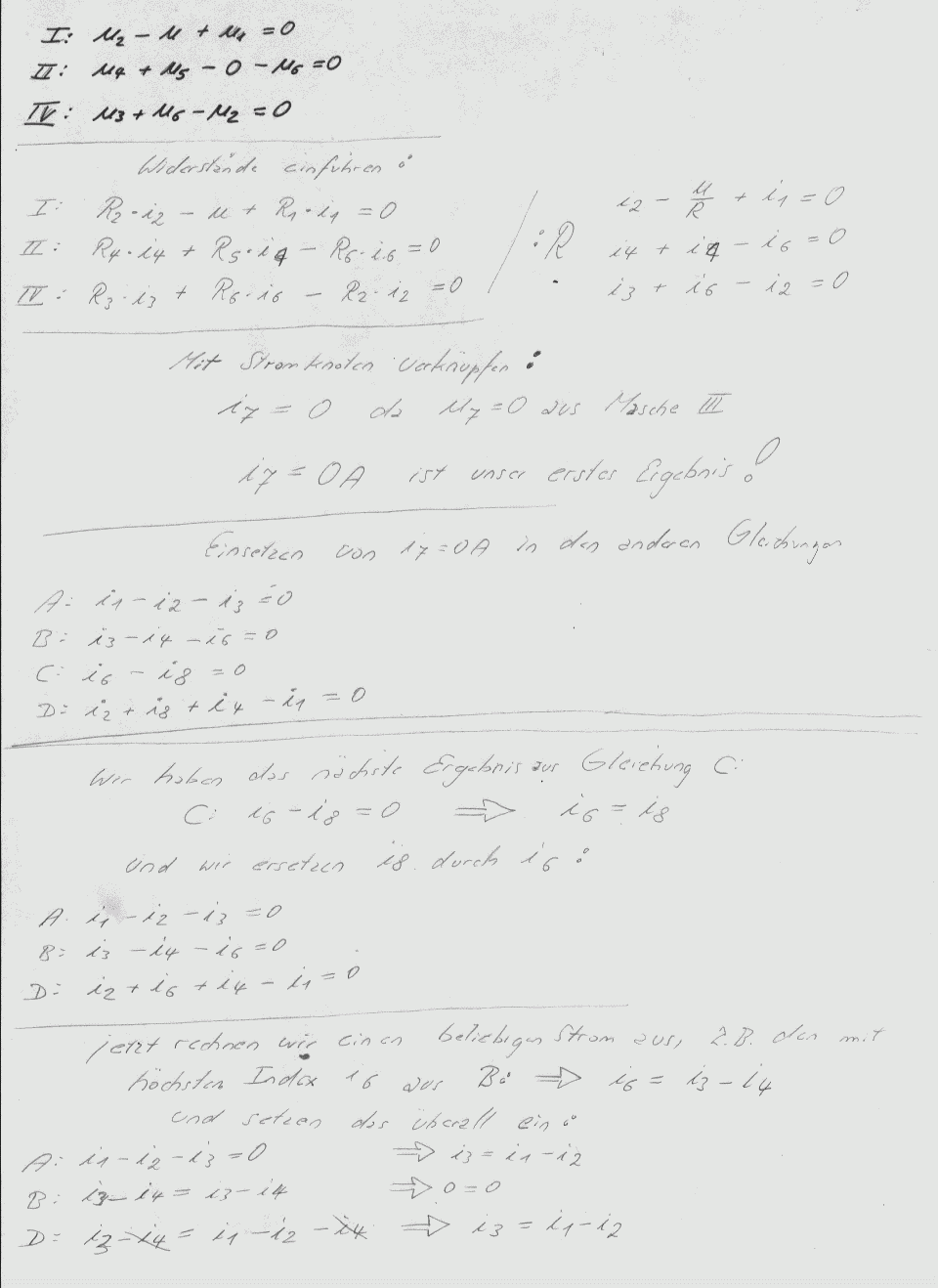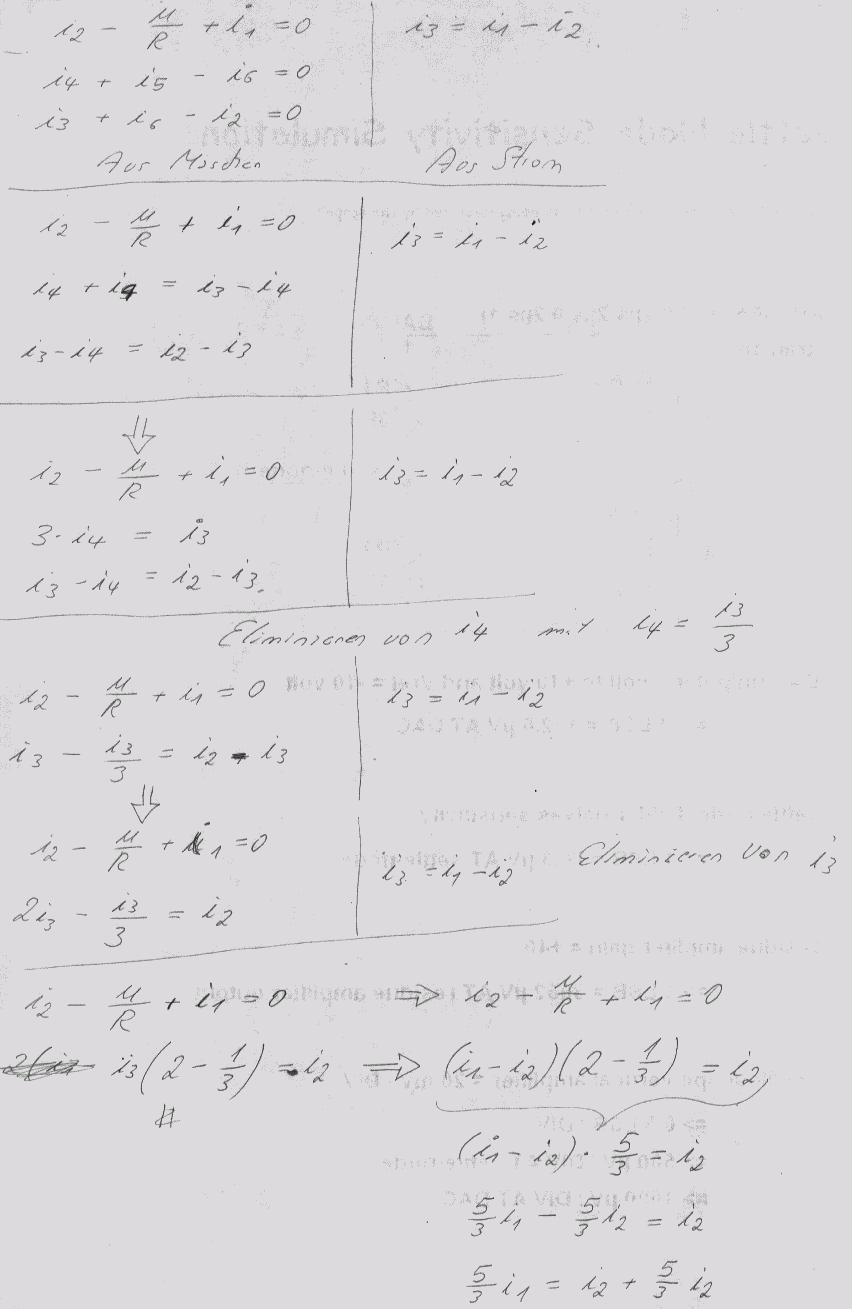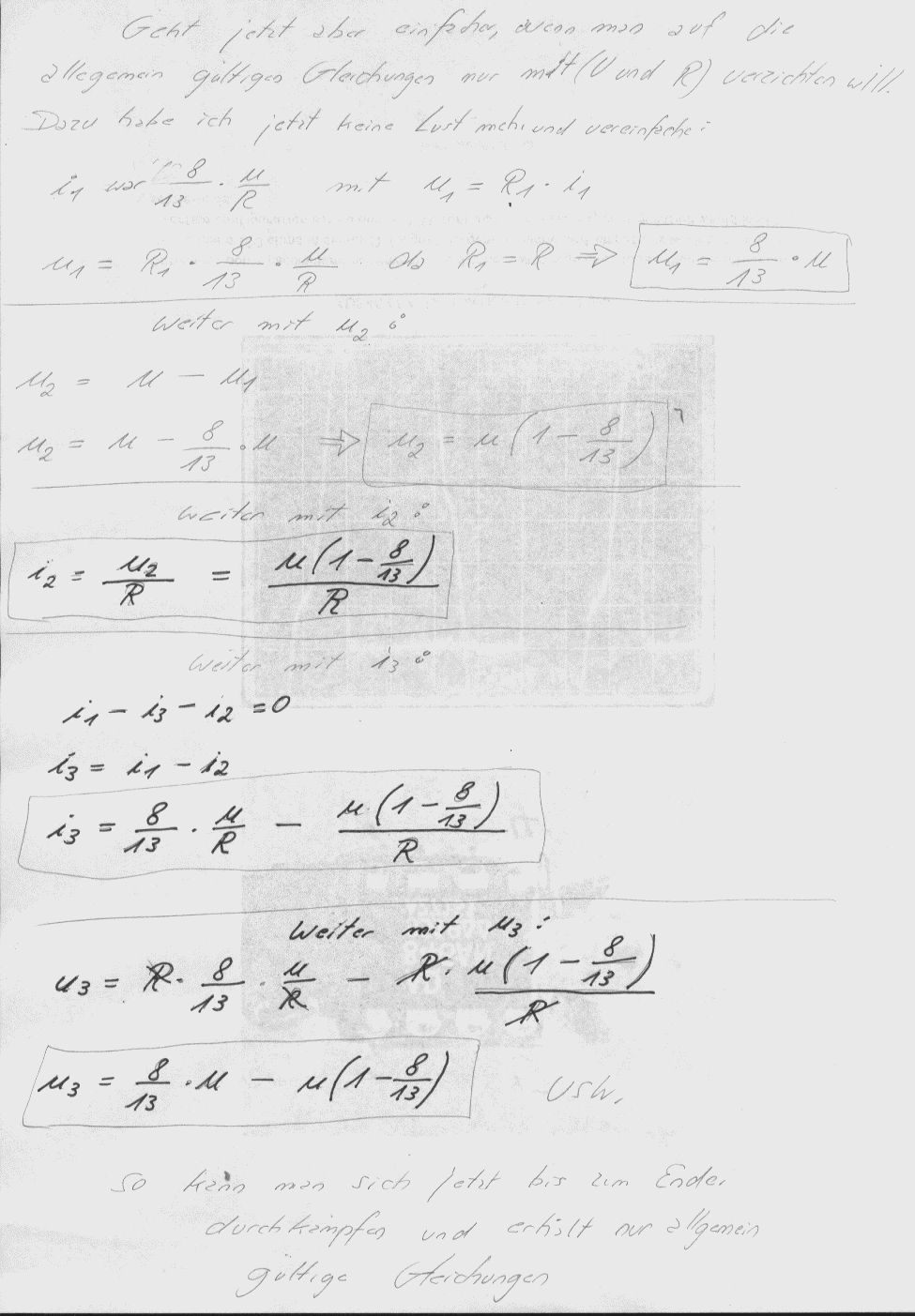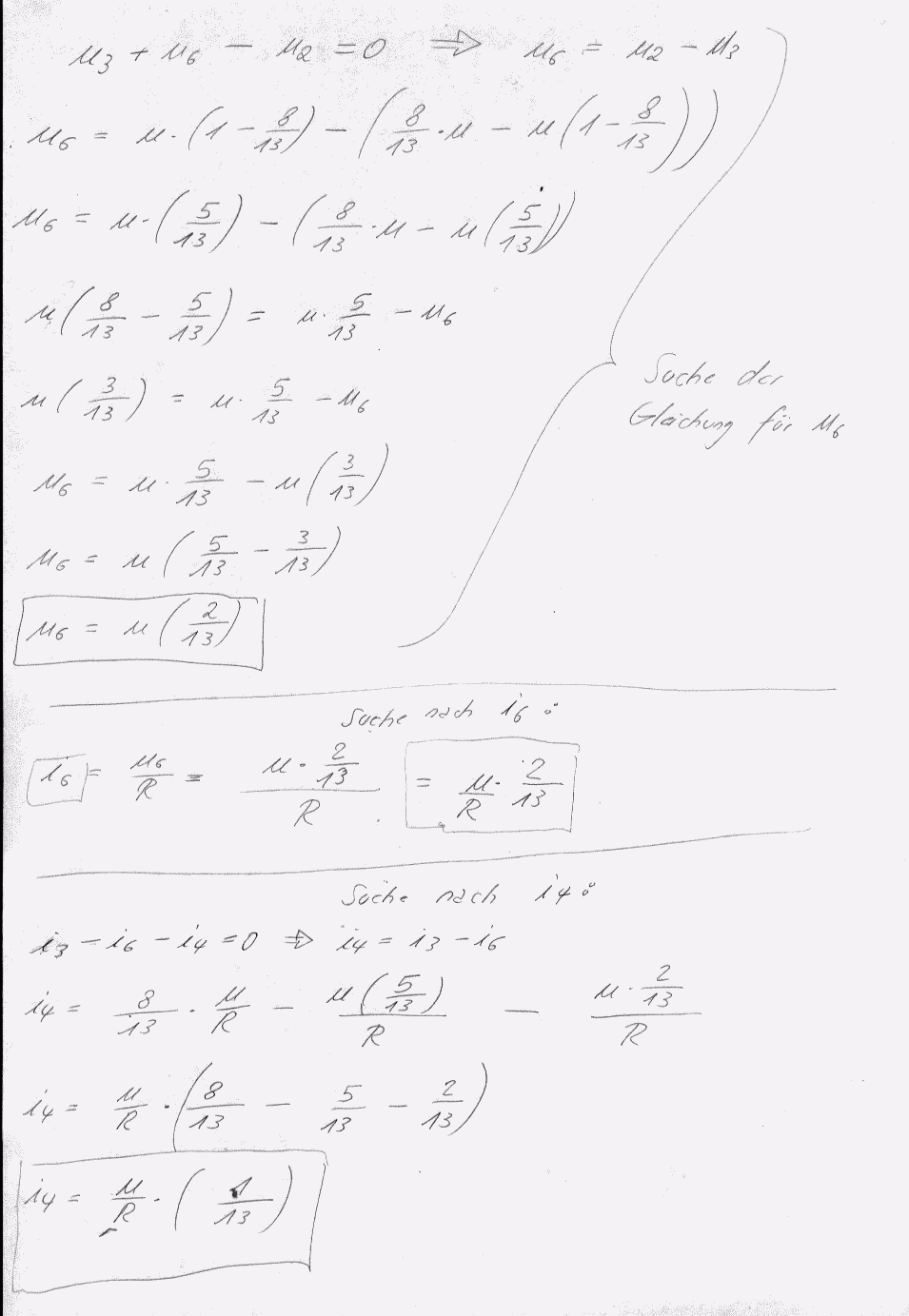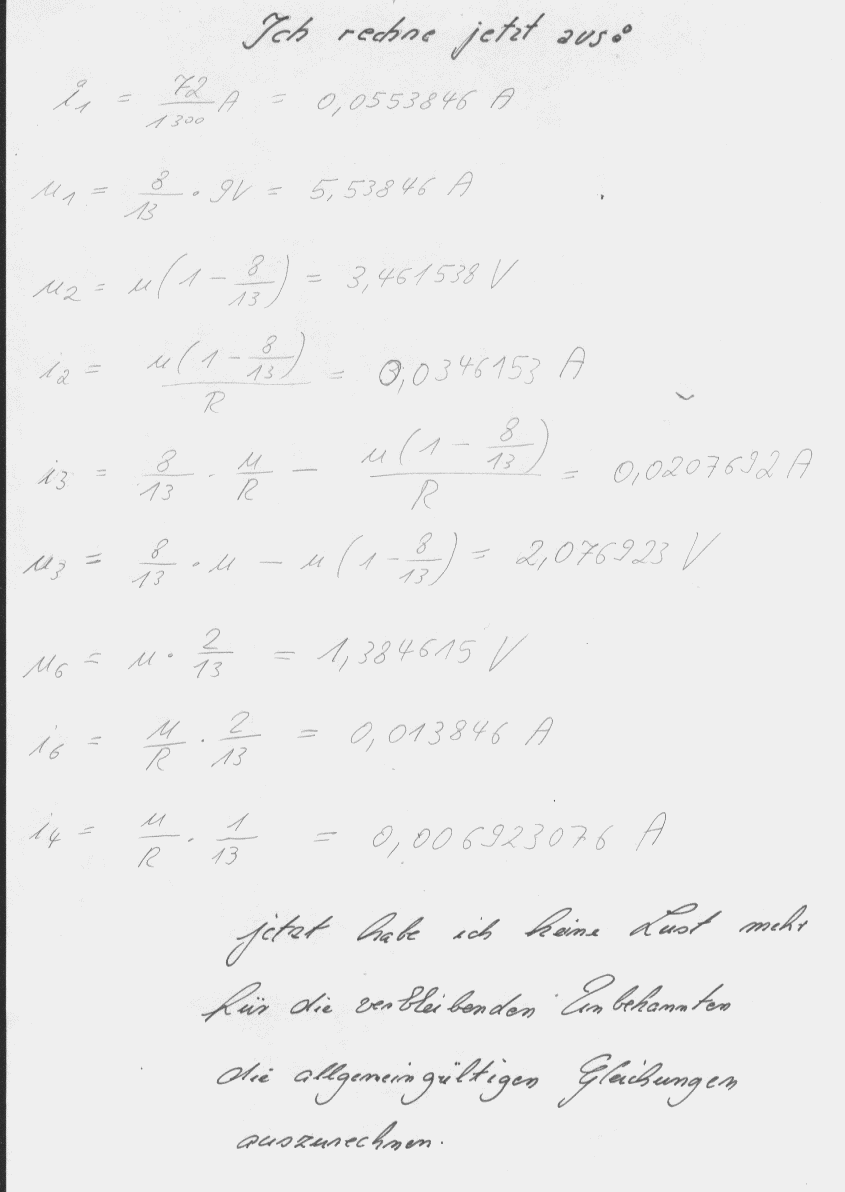Berechnung eines Netzwerkes mit Knoten und Maschen
Ein Leser fragte folgendes:
"Hallo,
ich behandle im Moment das Thema Elektrik. Dabei stoße ich im Moment auf das
Problem der Bestimmung von Stromstärken in beliebigen Schaltungen, die auch
Brückenschaltungen enthalten können.
Ich habe einiges gelesen, das mit der Knoten- und Maschenregel
von Kirchhoff zu tun hat und verstehe auch das grundsätzliche Vorgehen. Auf andere
Fälle angewendet ergeben sich aber bei mir Verständnisprobleme, so wie in der
beiliegenden Schaltung. Deshalb bin ich auf der Suche nach Hilfe. Die
Schaltung (beiliegende Abbildung) hat nur eine Spannungsquelle mit 9V und
besteht aus Lampen mir einem Widerstand von je 100 Ohm.
Welche Maschen bestehen hier drin und wo fließen welche Ströme?
Ich habe Probleme mit dieser Brücke, mein gefundenes Gleichungssystem lässt
sich nicht lösen?
Für jegliche Hilfe wäre ich sehr dankbar.
Viele Grüße
XY"
Ja was soll ich sagen, dann legen wir mal los:
Zunächst, persönlich halte
von solchen Aufgaben nix, da sie kaum zum Verständnis der
Elektrotechnik beitragen und viel mehr Mathematik Aufgaben sind, das
elektrotechnische Verständnis kaum fördern, sondern falls es
an der Mathematik klemmt nur frustrieren und das Gegenteil bewirken.
Was mich ganz besonders an solchen Aufgaben stört, sie basieren
nicht darauf sie nach klaren Verfahren zu lösen, sondern nur rein
durch elektrotechnische Überlegung an welcher Stelle vereinfacht
werden kann. Ich kann die folgende Schaltung auch rein durch
Überlegung über Vereinfachung lösen, in dem man
weiß, was man vereinfachen kann und vereinfachen darf. Um diese
Schaltung zu lösen brauche ich wenn ich will höchstens zwei
Minuten, sie richtig zu rechnen jedoch eine gute Stunde!
Als reine Rechenaufgabe um
sie über ein Gleichungssystem zu lösen ist sie zu
schwer, als reine Aufgabe zur Überlegung zu einfach
Was will ich damit sagen? Diese
Aufgabe wurde extra so konstruiert, dass man sie schon fast im Kopf
lösen kann, wenn man das Netzwerk geistig vereinfacht durch
Parallel- und Serienschaltungen der Einzelwiderstände, das soll
das Lernziel des ursprünglichen Authors sein. Jetzt stelle ich
aber die blöde Frage "was ist wenn es eine Schaltung ist, bei
deren Aufbau eine geistige Vereinfachbarkeit nicht möglich ist?"
Dann stehen genau diese Herren, die immer der Ansicht sind
"Fangaufgaben" den Anfängern stellen zu müssen ganz
schön blöde da, man kann sie nämlich nur durch berechnen
lösen.
Jetzt wollen wir sie mal rechnen, dazu gibt es mehre Verfahren wie die
Knoten- und Maschengleichungen hinterher aufzulösen sind. Die
eleganteste ist sicherlich der Weg lineare Gleichungssysteme über
Matrizen zu lösen, wobei ich da aber schon wieder ein Buch dazu
herauskramen müßte wie es zu Fuß zu rechnen ist. Der
HP 48 Rechner z.B. kann bei Zahlenwerten genau diese Matrizen
verarbeiten und spuckt dann wunderbar alle Ströme und Spannungen
als Matrix aus - bequemer geht es nicht.
Um es vorweg zu nehmen, seit dem Studium habe ich das Lösen von
solchen "Sinnlos" Netzwerken nicht mehr gemacht, noch nie gebraucht,
obwohl ich wirklich täglich übelste Elektronik mache. In der
Realität reichen Netzwerke der Größe von zwei drei
Maschen völlig aus, bei allem was darüber hinausgeht versagen
sowieso meist die Ansätze zur Modellierung des Systems. Man
darf solche Aufgaben nicht als Übungen zur Elektrotechnik
betrachten, sondern als reine Übungsaufgaben zur Mathematik und
dem Lösen von linearen Gleichungssystemen, mehr ist das nicht.
Zöum Lösen von linearen Gleichungssytemen, da kann der
Mathematiker viel mehr darüber sagen wie ich, man dann diese
unterteilen nach Anzahl der bekannten und unbekannten Variablen und
Gleichungen, überbestimmte Systemen und nach allem möglichem,
die Herren der Mathematik haben diese Angelegenheiten vollends im Griff
- ich brauch es nicht zu wissen, fall ich es doch mal für eine
elektrotechnische Aufbage unbedingt sehr genau wissen muss, dafür
gibt es Mathematik Bücher, alles andere ist für mich
persönlich Zeitverschwendung, Zeiten in denen ich eine Schaltung
machen kann.
Der einzige Sinn, den man in solchen Aufgaben sehen kann wäre nicht die Frage:
"Berechnen Sie alle Ströme und Spannungen"
- sondern -
"Vereinfachen sie das
Netzwerk geistig so weit als möglich, um es dann möglichst
einfach ohne die Anwendung von starrer Mathematik (Knoten und Maschen)
schnell ausrechen zu können".
Solche "Fangaufgaben" per
Knoten- und Maschenregeln mit anschließender
Gleichungseliminierung zu lösen betrachte ich als eine
Strafarbeit, die ich mir jetzt aber mal an tun werde und erhalte
dafür als Belohnung allgemeingültige Gleichungen, in die man
U und R einsetzen kann.
Schaltung:
Bei Schaltungen, bei denen Birnchen
anstatt Widerstände eingezeichnet sind ist schon mal Vorsicht
angesagt, die Steigerung ist dann immer noch die Tatsache wenn auf den
Knoten die Lötpunkte fehlen (bei der mir zugesandten Schaltung
fehlten die, nur kann ich das so nicht nachmalen - das geht nicht -
wäre ein Prinzipien Bruch, die Birnchen zu malen, dazu konnte man
mich hier überreden, obwohl ein Widerstandssymbol besser
wäre. In aller Regel ist es so, wer in Schaltungen die Punkte an
den Knoten nicht einzeichnet - vergiss die diese Schaltungen - es sind
die Erfahrungen, die man damit schon gemacht hat und diese Worte auf's
Papier bringen.
Aufgabe: eine Betriebsspannung von 9 Volt, alle Widerstände
gleicher Widerstandswert mit 100 Ohm, berechen alle Ströme und
Spannungen.
Zunöchst sollte man sich das Gebilde so umzeichen, dass man es
besser versteht, das soll jeder so machen wie er will. Dann Anwendung
der
Knoten- und
Maschenregeln.
Die folgenden Blätter habe ich frei ohne sonderlich zu
überlegen hingeschrieben. Wenn man jeden Schritt hinschreibt,
vermindert sich die Gefahr von Flüchtigkeitsfehlern.
Sorry dummerweise, habe ich die Rechnung mit einem dünnen
Bleistift gemacht, was zu schlechten Scans führt, es aber noch mal
abschreiben mit dickem Stift will ich nicht mehr - Du musst
es sowieso selber noch rechnen.
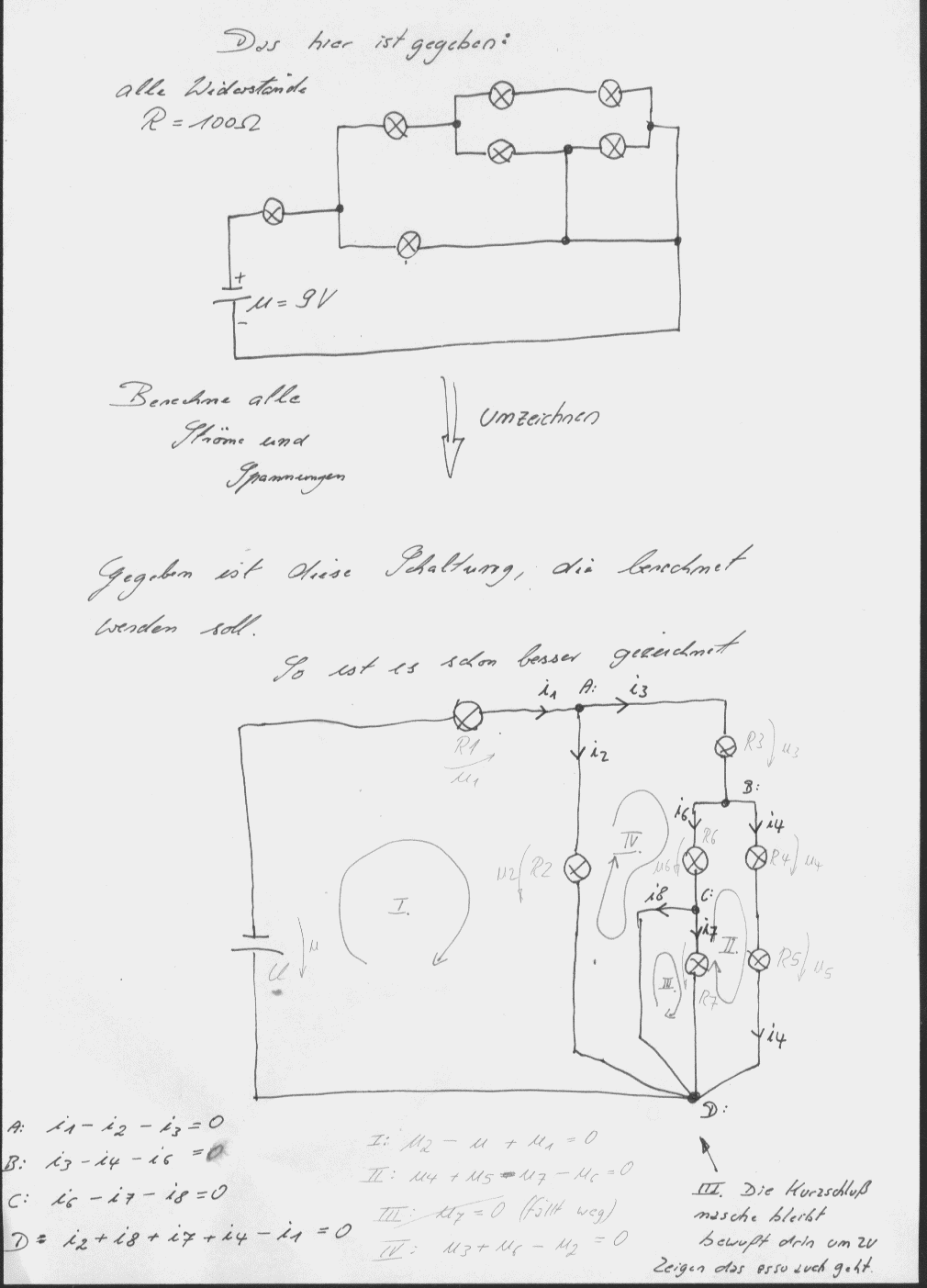
Die Buchstaben A, B, C und D sind die
Stromknoten des Netzwerks, normalerweise reicht es n-1 Knoten zu
nehmen, der überbestimmte Knoten fliegt sowieso später immer
raus. Aber nicht schlimm, es ist mathematisch nicht falsch ihn
drinzulassen.
Die römischen Zahlen I. bis IV bezeichnen die Spannungsmaschen. Es
sind jeweils die Kernmaschen anzuwenden (engste Maschen).
Ganz bewußt wurde hier die Spannungsmasche III in der Berechnung
drin gelassen, um zu zeigen dass selbst wenn man diese schwachsinnige
Kurzschlußmasche mathematisch drin läßt, es noch
richtig ist mit ihr zu rechnen, sie fällt später von alleine
raus, wenn man stur ohne zu denken rechnet. Diese
Kurzschlußmasche zu erkennen und zu eliminieren wäre der
erste Ansatz beim Lösen der Aufgabe nach der Methode der
"geistigen Überlegung nach Vereinfachungen". Das Rechen mit
Knoten- und Maschen ist idiotensicher und funktioniert immer, klappt
auch Nachts um Halb vier in halbwachem Zustand, allerdings bei
Netzwerken mit so vielen Elemtenen wie in dieser Schaltung ist es eine
Strafarbeit und normalerweise eine Arbeit für einen Computer.
Jetzt geht das Verrechnen los, die Kommentare stehen in den Bildern:
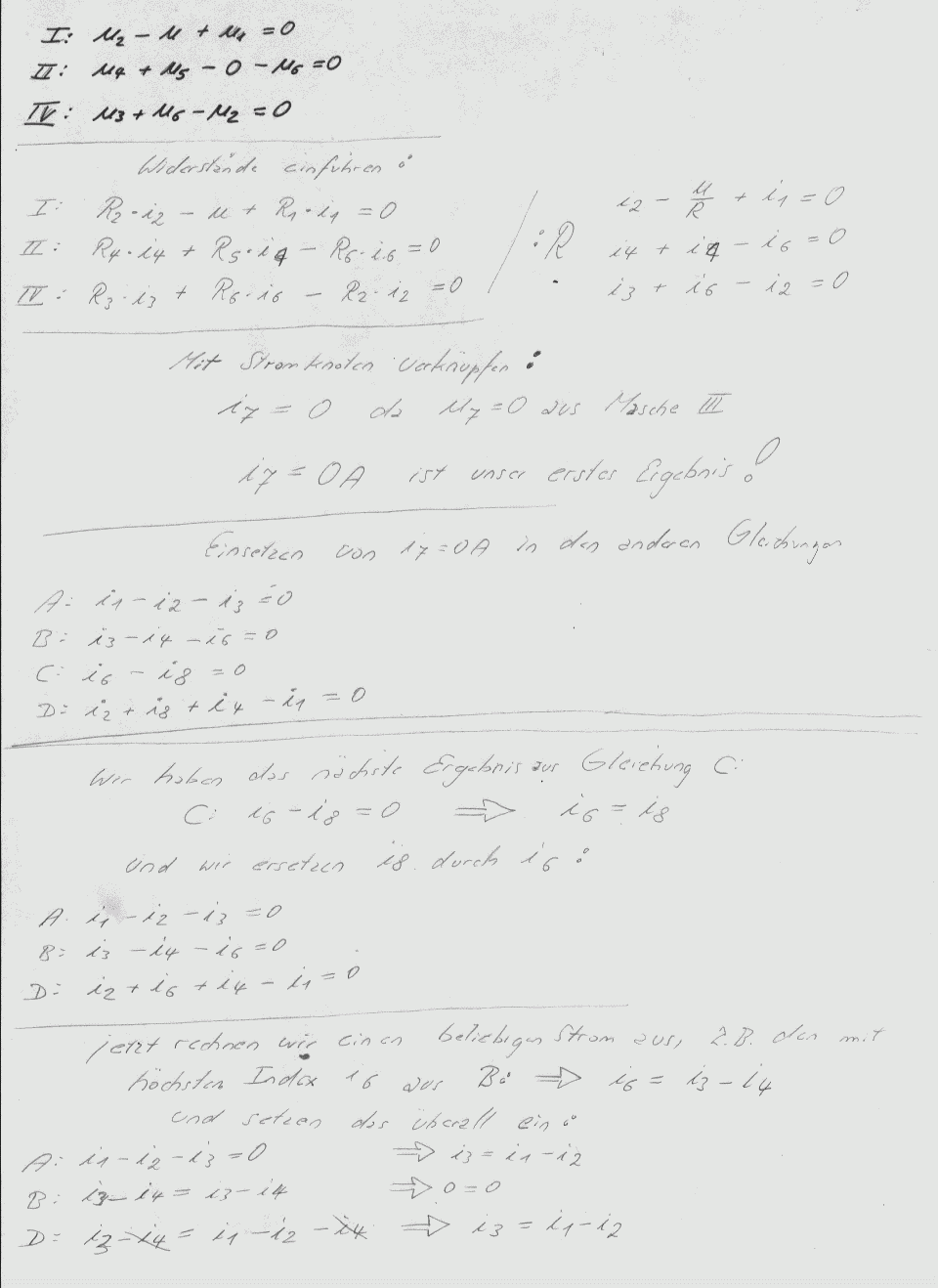
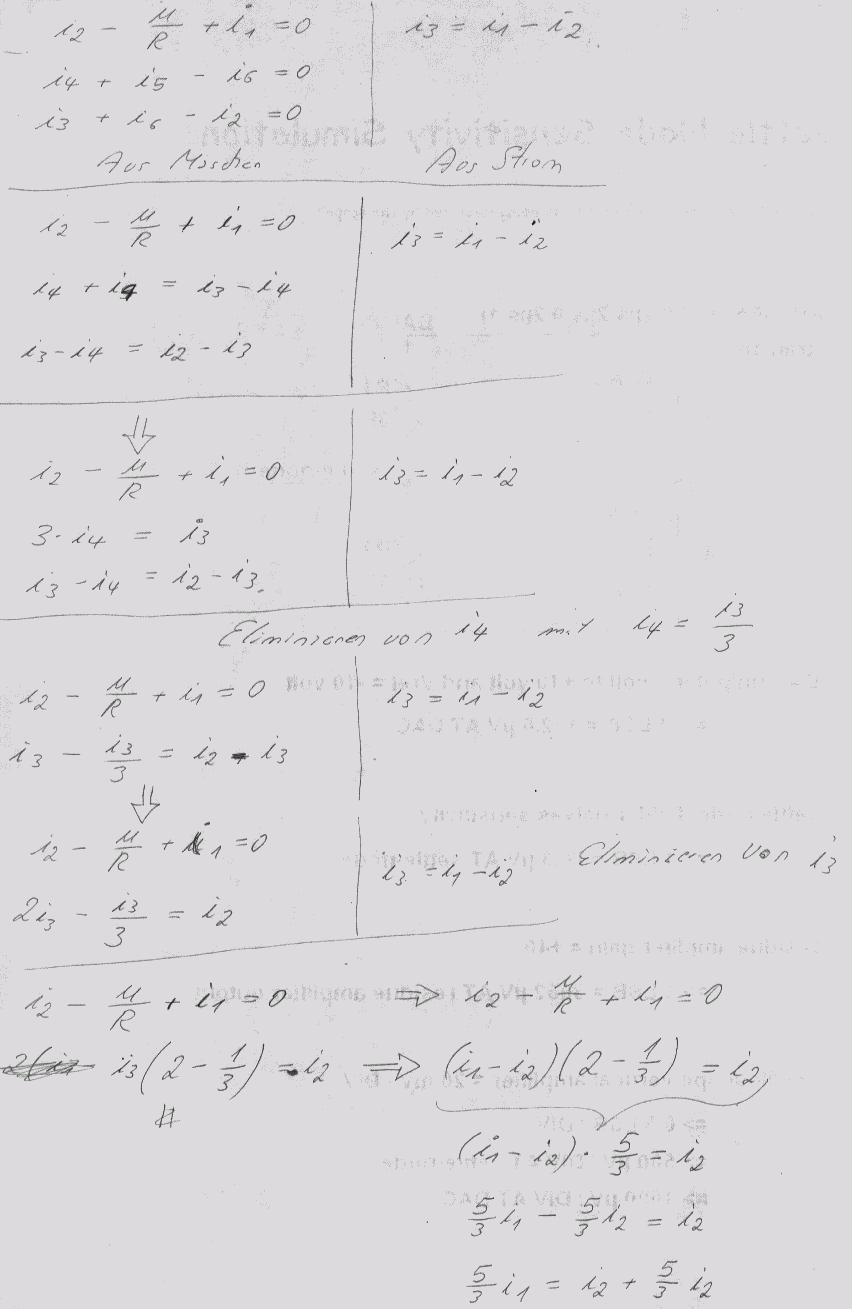

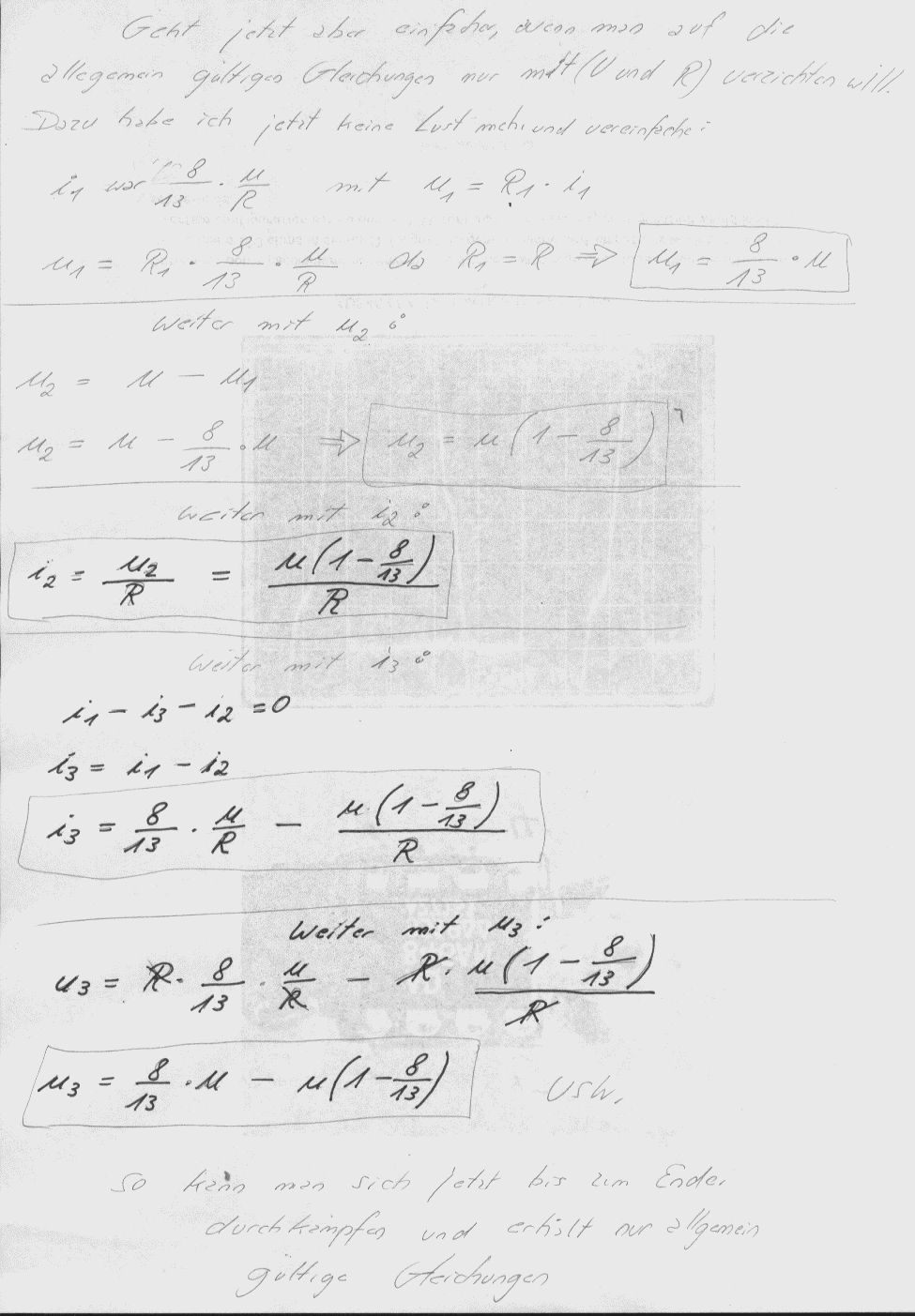
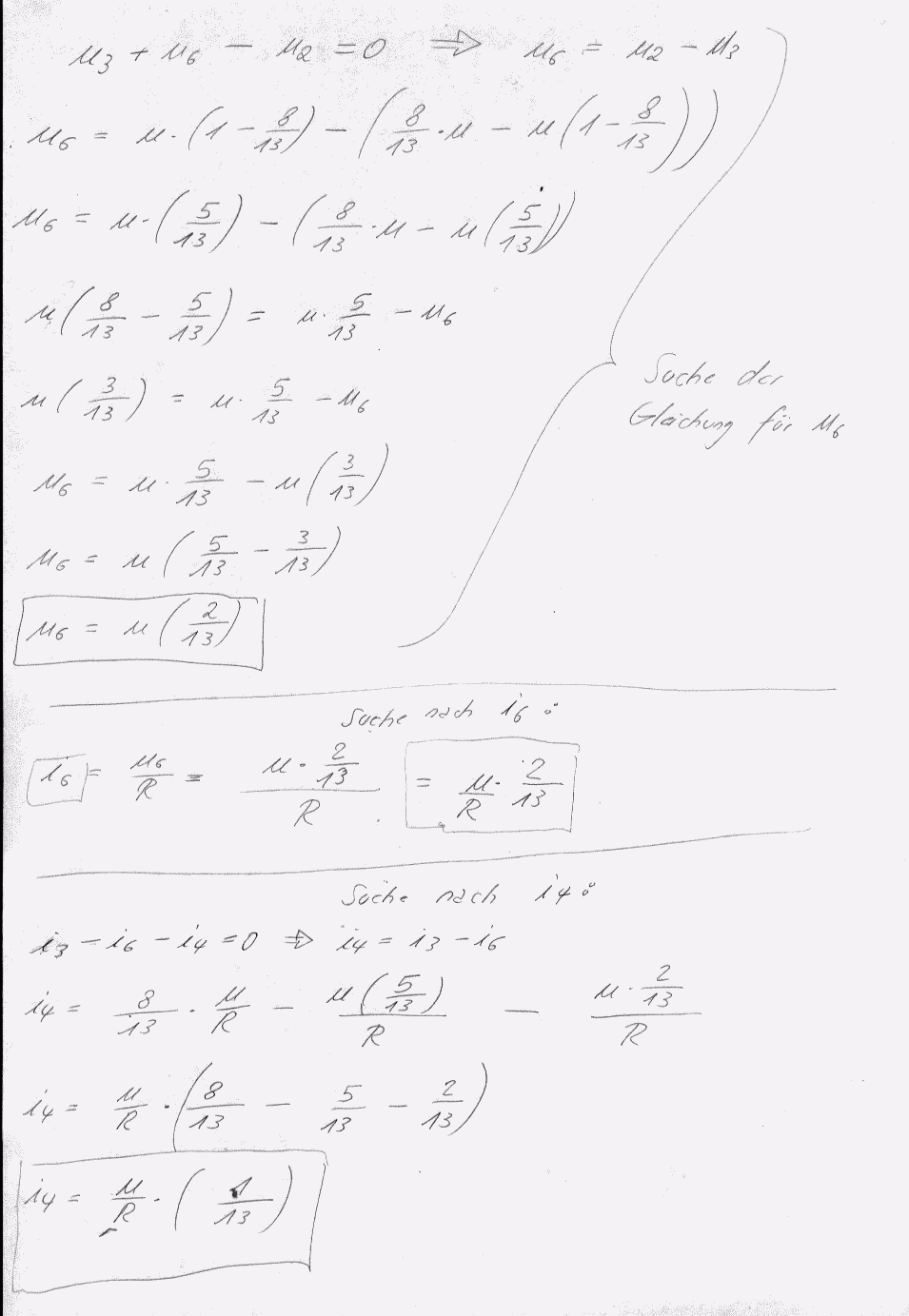
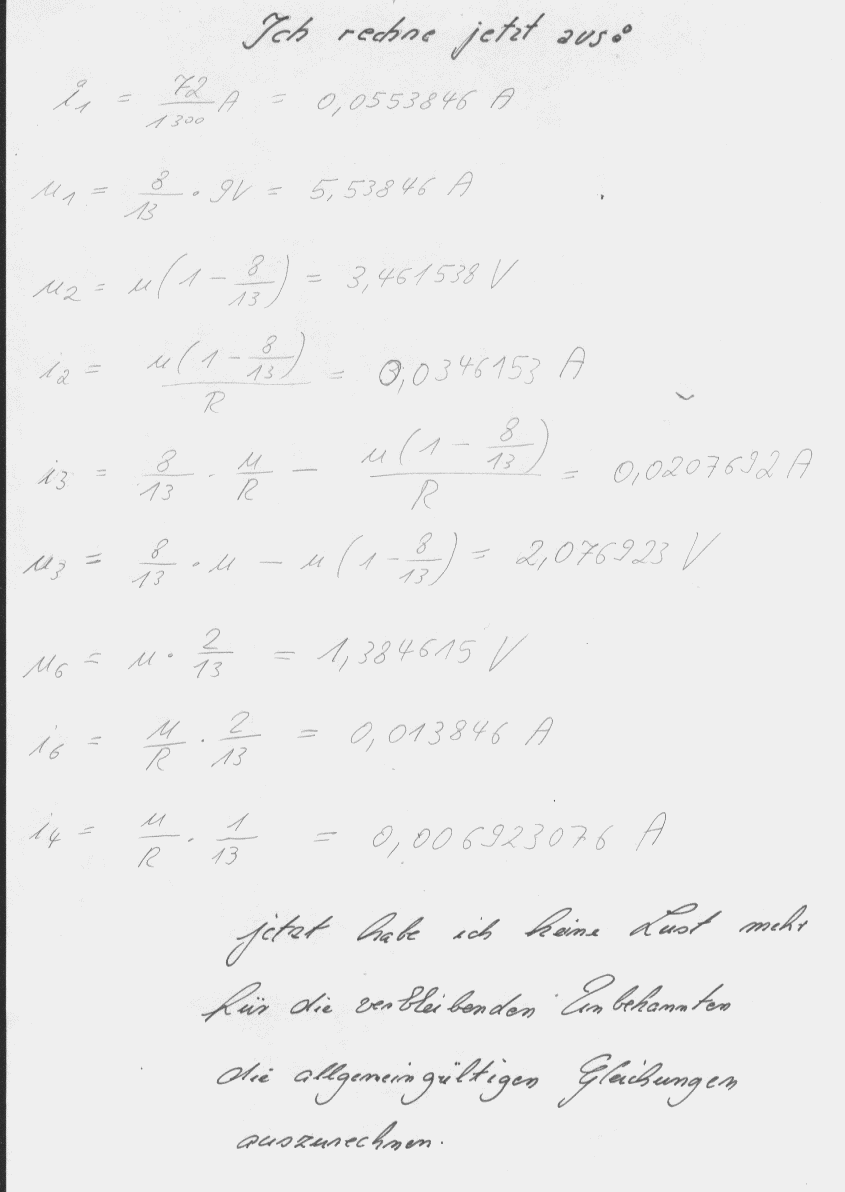
Ganz schön heftig oder ? Wenn man dieses Netzwerk allgemeingültig ausrechnen will.
Um zu zeigen wie einfach es durch reine Überlegung geht die folgenden Scans:
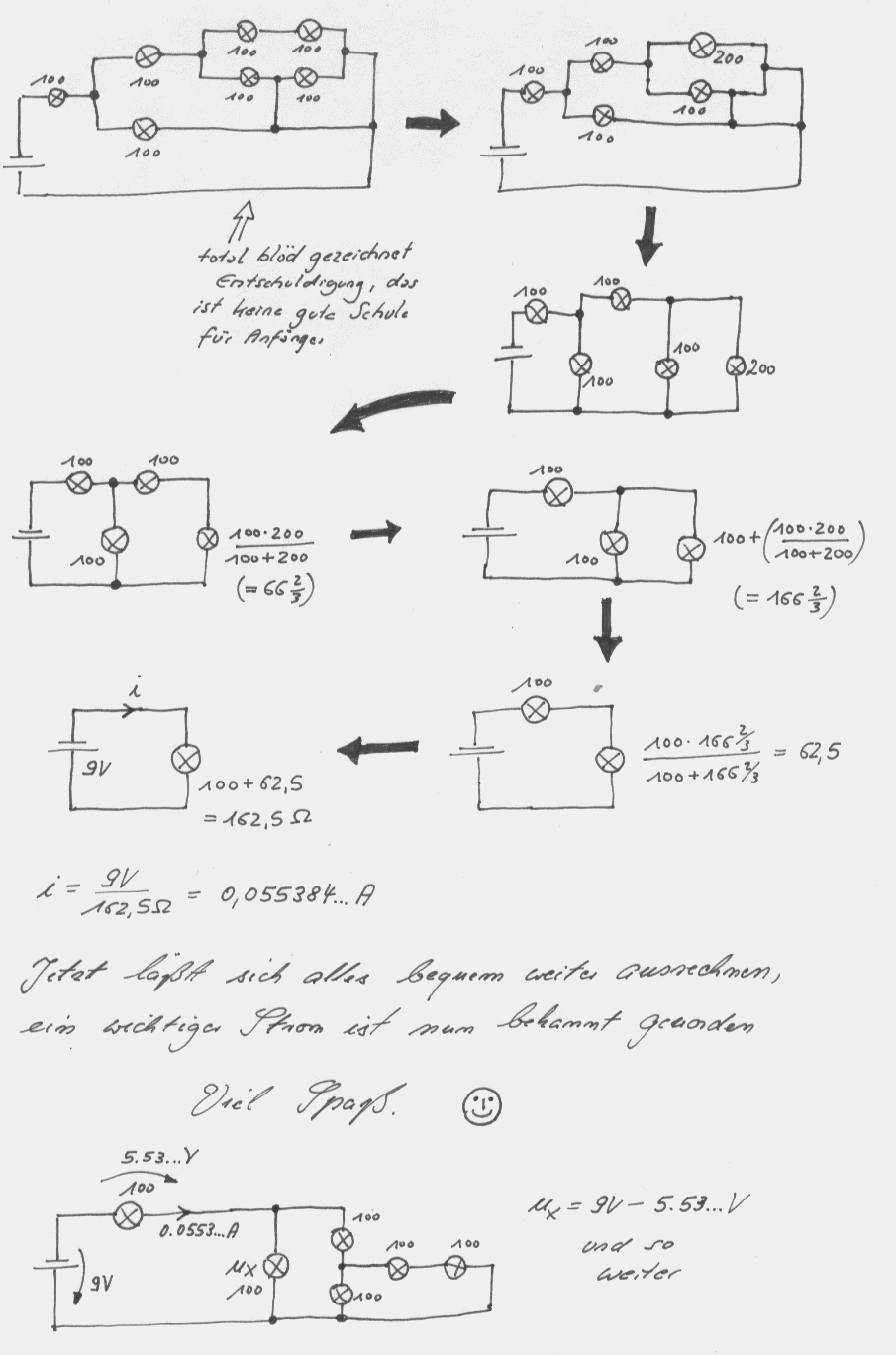
"Als reine Rechenaufgabe um
sie über ein Gleichungssystem zu lösen ist sie zu
schwer, als reine Aufgabe zur Überlegung zu einfach".
Ich denke dieser Satz kann jetzt nachvollzogen werden.

Impressum und Haftungsausschluss